如图，EF∥AD，∠1∠2，∠BAC80°，将求∠AGD的过

首页 / 初中数学 / 试题详细

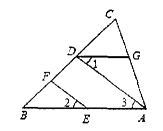
如图，EF∥AD，∠1=∠2，∠BAC=80°，将求∠AGD的过程填写完整．
∵EF//AD，
∴∠2=   （   ）
又∵∠1=∠2，
∴∠1=∠3（   ）
∴AB//   （   ）
∴∠BAC＋   =180°（   ）
∵∠BAC=80°，
∴∠AGD=

登录免费查看答案和解析

相关试题

据公开报道，2017年全国教育经费总投入为42557亿元，比上年增长 $9.43 %$ ，其中投入在各学段的经费占比（即所占比例）如图，根据图中提供的信息解答下列问题．

（1）在2017年全国教育经费总投入中，义务教育段的经费总投入应该是多少亿元？

（2）2016年全国教育经费总投入约为多少亿元？（精确到 $0.1)$

收藏答案/解析

已知： $∠ AOB$ ．

求作： $∠ A' O' B'$ ，使得 $∠ A' O' B' = ∠ AOB$ ．

作法：

①以 $O$ 为圆心，任意长为半径画弧，分别交 $OA$ ， $OB$ 于点 $C$ ， $D$ ；

②画一条射线 $O' A'$ ，以点 $O'$ 为圆心， $OC$ 长为半径画弧，交 $O' A'$ 于点 $C'$ ；

③以点 $C'$ 为圆心， $CD$ 长为半径画弧，与第②步中所画的弧相交于点 $D'$ ；

④过点 $D'$ 画射线 $O' B'$ ，则 $∠ A' O' B' = ∠ AOB$ ．

根据上面的作法，完成以下问题：

（1）使用直尺和圆规，作出 $∠ A' O' B'$ （请保留作图痕迹）．

（2）完成下面证明 $∠ A' O' B' = ∠ AOB$ 的过程（注 $:$ 括号里填写推理的依据）．

证明：由作法可知 $O' C' = OC$ ， $O' D' = OD$ ， $D' C' =$ 　　，

$∴$ △ $C' O' D' ≅ ΔCOD ($ 　　 $)$

$∴ ∠ A' O' B' = ∠ AOB$ ． $($ 　　 $)$

收藏答案/解析

如图，在平面直角坐标系中，已知点 $B$ 的坐标为 $(- 1, 0)$ ，且 $OA = OC = 4 OB$ ，抛物线 $y = a x^{2} + bx + c (a \neq 0)$ 图象经过 $A$ ， $B$ ， $C$ 三点．

（1）求 $A$ ， $C$ 两点的坐标；

（2）求抛物线的解析式；

（3）若点 $P$ 是直线 $AC$ 下方的抛物线上的一个动点，作 $PD ⊥ AC$ 于点 $D$ ，当 $PD$ 的值最大时，求此时点 $P$ 的坐标及 $PD$ 的最大值．

收藏答案/解析

如图， $BD$ 是 $⊙ O$ 的直径，弦 $BC$ 与 $OA$ 相交于点 $E$ ， $AF$ 与 $⊙ O$ 相切于点 $A$ ，交 $DB$ 的延长线于点 $F$ ， $∠ F = 30 °$ ， $∠ BAC = 120 °$ ， $BC = 8$ ．

（1）求 $∠ ADB$ 的度数；

（2）求 $AC$ 的长度．

收藏答案/解析

如图，在矩形 $ABCD$ 中， $E$ ， $F$ 分别是 $BC$ ， $AD$ 边上的点，且 $AE = CF$ ．

（1）求证： $ΔABE ≅ ΔCDF$ ；

（2）当 $AC ⊥ EF$ 时，四边形 $AECF$ 是菱形吗？请说明理由．

收藏答案/解析

推荐套卷

热门套卷