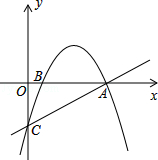已知直线y=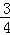 x﹣3与x轴交于点A,与y轴交于点C,抛物线y=﹣
x﹣3与x轴交于点A,与y轴交于点C,抛物线y=﹣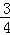 x2+mx+n经过点A和点C.
x2+mx+n经过点A和点C.
(1)求此抛物线的解析式;
(2)在直线CA上方的抛物线上是否存在点D,使得△ACD的面积最大?若存在,求出点D的坐标;若不存在,说明理由.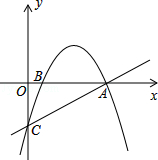
相关知识点
推荐套卷
已知直线y=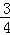 x﹣3与x轴交于点A,与y轴交于点C,抛物线y=﹣
x﹣3与x轴交于点A,与y轴交于点C,抛物线y=﹣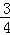 x2+mx+n经过点A和点C.
x2+mx+n经过点A和点C.
(1)求此抛物线的解析式;
(2)在直线CA上方的抛物线上是否存在点D,使得△ACD的面积最大?若存在,求出点D的坐标;若不存在,说明理由.