古希腊毕达哥拉斯学派的数学家研究过各种多边形数。如三角形数1,3,6,10···，第n个三角形数为
。记第n个k边形数为N(n,k)(
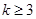),以下列出了部分k边形数中第n个数的表达式：
三角形数 N(n,3)=
正方形数 N(n,4)=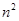
五边形数 N(n,5)=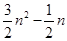
六边形数 N(n,6)=
可以推测N(n,k)的表达式，由此计算N(10,24)= ____________
中，
，则
．
，
成等比数列，则
．
有三个不同的零点，则实数
的取值范围是 ．
与曲线
相切于点
，则
的值为 ．
，则f（x）dx
．相关知识点
推荐套卷
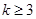古希腊毕达哥拉斯学派的数学家研究过各种多边形数。如三角形数1,3,6,10···，第n个三角形数为。记第n个k边形数为N(n,k)(),以下列出了部分k边形数中第n个数的表达式：
三角形数 N(n,3)=
正方形数 N(n,4)=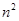
五边形数 N(n,5)=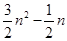
六边形数 N(n,6)=
可以推测N(n,k)的表达式，由此计算N(10,24)= ____________
粤公网安备 44130202000953号