阅读下面的例题,并回答问题.
【例题】解一元二次不等式:x2-2x-8>0.
解:对x2-2x-8分解因式,得x2-2x-8=(x-1)2-9=(x-1)2-32=(x+2)(x-4),
∴(x+2)(x-4)>0.由“两实数相乘,同号得正,异号得负”,可得 ①或
①或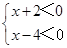 ②
②
解①得x>4;解②得x<-2.
故x2-2x-8>0的解集是x>4或x<-2.
(1)直接写出x2-9>0的解是 ;
(2)仿照例题的解法解不等式:x2+4x-21<0;
(3)求分式不等式: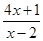 ≤0的解集.
≤0的解集.
相关知识点
推荐套卷
 ,延长OE到点F,使EF=2OE.
,延长OE到点F,使EF=2OE.
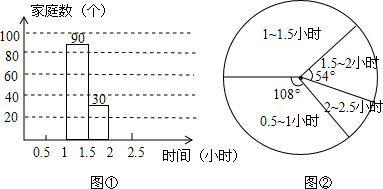
 .
.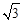 ≈1.732,结果保留三个有效数字).
≈1.732,结果保留三个有效数字).
 粤公网安备 44130202000953号
粤公网安备 44130202000953号