高二某班50名学生在一次百米测试中,成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组[13,14),第二组[14,15)…第五组[17,18],如图是按上述分组方法得到的频率分布直方图.
(1)若成绩大于等于14秒且小于16秒规定为良好,求该班在这次百米测试中成绩为良好的人数.
(2)请根据频率分布直方图,估计样本数据的众数和中位数(精确到0.01).
(3)设 表示该班两个学生的百米测试成绩,已知
表示该班两个学生的百米测试成绩,已知 ,求事件
,求事件 的概率.
的概率.
相关知识点
推荐套卷
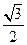 ,
,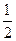 ,0),点D在平面yoz上,且
,0),点D在平面yoz上,且 BDC=900,
BDC=900,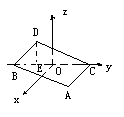
 粤公网安备 44130202000953号
粤公网安备 44130202000953号