六•一儿童节,小文到公园游玩,看到公园的一段人行弯道MN(不计宽度),如图,它与两面互相垂直的围墙OP、OQ之间有一块空地MPOQN(MP⊥OP,NQ⊥OQ),他发现弯道MN上任一点到两边围墙的垂线段与围墙所围成的矩形的面积相等,比如:A、B、C是弯道MN上任三点,矩形ADOG、矩形BEOH、矩形CFOI的面积相等. 爱好数学的他建立了平面直角坐标系(如图).图中三块阴影部分的面积分别记为S1、S2、S3,并测得S2=6(单位:平方米),OG=GH=HI.
(1)求S1和S3的值;
(2)设T 是弯道MN上的任一点,写出y关于x的函数关系式;
是弯道MN上的任一点,写出y关于x的函数关系式;
(3)公园准备对区域MPOQN内部进行绿化改选,在横坐标、纵坐标都是偶数的点处种植花木(区域边界上的点除外),已知MP=2米,NQ=3米.问一共能种植多少棵花木?
相关知识点
推荐套卷
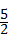 KC,求
KC,求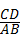 的值;
的值;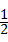 AD时,猜想线段AB、BC、CD三者之间有怎样的等量关系?请写出你的结论并予以证明.再探究:当AE=
AD时,猜想线段AB、BC、CD三者之间有怎样的等量关系?请写出你的结论并予以证明.再探究:当AE=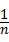 AD(n>2),而其余条件不变时,线段AB、BC、CD三者之间又有怎样的等量关系?请直接写出你的结论,不必证明.
AD(n>2),而其余条件不变时,线段AB、BC、CD三者之间又有怎样的等量关系?请直接写出你的结论,不必证明.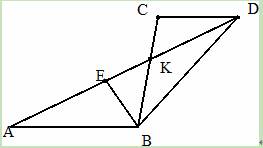
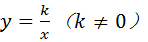 的图象经过点(
的图象经过点(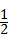 ,8),直线y=﹣x+b经过该反比例函数图象上的点Q(4,m).
,8),直线y=﹣x+b经过该反比例函数图象上的点Q(4,m).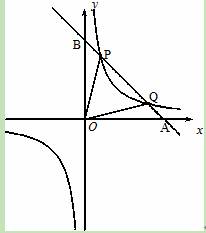
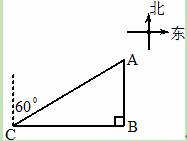
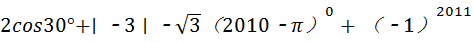 .
.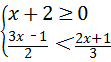 ,并写出该不等式组的最小整数解.
,并写出该不等式组的最小整数解. 粤公网安备 44130202000953号
粤公网安备 44130202000953号