为了了解某地初中三年级学生参加消防知识竞赛成绩(均为整数),从中抽取了1%的同学的竞赛成绩,整理后绘制了如下的频数分布直方图,请结合图形解答下列问题:
(1)指出这个问题中的总体;
(2)求竞赛成绩在84.5﹣89.5这一小组的频率;
(3)如果竞赛成绩在90分以上(含90分)的同学可以获得奖励,请估计该地初三年级约有多少人获得奖励.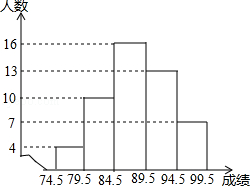
相关知识点
推荐套卷
为了了解某地初中三年级学生参加消防知识竞赛成绩(均为整数),从中抽取了1%的同学的竞赛成绩,整理后绘制了如下的频数分布直方图,请结合图形解答下列问题:
(1)指出这个问题中的总体;
(2)求竞赛成绩在84.5﹣89.5这一小组的频率;
(3)如果竞赛成绩在90分以上(含90分)的同学可以获得奖励,请估计该地初三年级约有多少人获得奖励.