如图,已知∠MON=90°,A是∠MON内部的一点,过点A作AB⊥ON,垂足为点B,AB=3厘米,OB=4厘米,动点E,F同时从O点出发,点E以1.5厘米/秒的速度沿ON方向运动,点F以2厘米/秒的速度沿OM方向运动,EF与OA交于点C,连接AE,当点E到达点B时,点F随之停止运动.设运动时间为t秒(t>0).
(1)当t=1秒时,△EOF与△ABO是否相似?请说明理由;
(2)在运动过程中,不论t取何值时,总有EF⊥OA.为什么?
(3)连接AF,在运动过程中,是否存在某一时刻t,使得S△AEF= S四边形ABOF?若存在,请求出此时t的值;若不存在,请说明理由.
S四边形ABOF?若存在,请求出此时t的值;若不存在,请说明理由.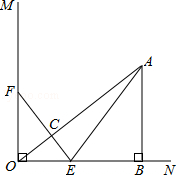
推荐套卷



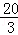


 粤公网安备 44130202000953号
粤公网安备 44130202000953号