如图，在矩形ABCD中，AD=
AB，∠BAD的平分线交BC于点E，DH⊥AE于点H，连接BH并延长交CD于点F，连接DE交BF于点O，下列结论：
①∠AED=∠CED；②OE=OD；③BH=HF；④BC﹣CF=2HE；⑤AB=HF，
其中正确的有（ ）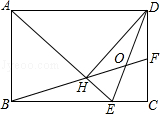
| A．2个 | B．3个 | C．4个 | D．5个 |
有实数根，则k的取值范围是 （ ）
时可配方得 （ ）
成立，那么x的取值范围是 ( )
推荐套卷
如图，在矩形ABCD中，AD=AB，∠BAD的平分线交BC于点E，DH⊥AE于点H，连接BH并延长交CD于点F，连接DE交BF于点O，下列结论：
①∠AED=∠CED；②OE=OD；③BH=HF；④BC﹣CF=2HE；⑤AB=HF，
其中正确的有（ ）
| A．2个 | B．3个 | C．4个 | D．5个 |
粤公网安备 44130202000953号