如图1，点A是线段BC上一点，△ABD和△ACE都是等边三角形．
（1）连结BE，CD，求证：BE=CD；
（2）如图2，将△ABD绕点A顺时针旋转得到△AB′D′．
①当旋转角为 度时，边AD′落在AE上；
②在①的条件下，延长DD’交CE于点P，连接BD′，CD′．当线段AB、AC满足什么数量关系时，△BDD′与△CPD′全等？并给予证明．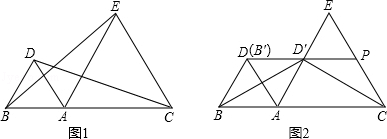
相关试题
推荐套卷
如图1，点A是线段BC上一点，△ABD和△ACE都是等边三角形．
（1）连结BE，CD，求证：BE=CD；
（2）如图2，将△ABD绕点A顺时针旋转得到△AB′D′．
①当旋转角为 度时，边AD′落在AE上；
②在①的条件下，延长DD’交CE于点P，连接BD′，CD′．当线段AB、AC满足什么数量关系时，△BDD′与△CPD′全等？并给予证明．
粤公网安备 44130202000953号