某校在高二年级开设了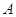 ,
,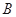 ,
,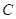 三个兴趣小组,为了对兴趣小组活动的开展情况进行调查,用分层抽样方法从
三个兴趣小组,为了对兴趣小组活动的开展情况进行调查,用分层抽样方法从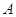 ,
,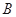 ,
,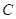 三个兴趣小组的人员中,抽取若干人组成调查小组,有关数据见下表(单位:人)
三个兴趣小组的人员中,抽取若干人组成调查小组,有关数据见下表(单位:人)
| 兴趣小组 |
小组人数 |
抽取人数 |
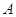 |
12 |
 |
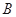 |
36 |
3 |
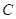 |
48 |
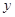 |
(1)求 ,
,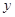 的值;
的值;
(2)若从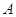 ,
,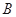 两个兴趣小组所抽取的人中选2人作专题发言,求这2人都来自兴趣小组
两个兴趣小组所抽取的人中选2人作专题发言,求这2人都来自兴趣小组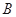 的概率.
的概率.
相关知识点
推荐套卷
 取
取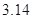 );
);
 A∩B,A∩C=
A∩B,A∩C=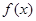 是定义在
是定义在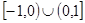 上的奇函数,当
上的奇函数,当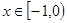 时,
时, 为实数);
为实数); 时,求函数
时,求函数 ,试判断
,试判断 上的单调性;
上的单调性;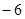 。
。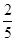 ,其中有一半会晕机,而女乘客只有
,其中有一半会晕机,而女乘客只有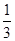 的人会晕机,经过调查员的计算:有95%以上的把握认为是否晕机与性别有关,那么被调查的人中最少有多少人会晕机? 参考: P(k
的人会晕机,经过调查员的计算:有95%以上的把握认为是否晕机与性别有关,那么被调查的人中最少有多少人会晕机? 参考: P(k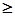 3.841)=0.05
3.841)=0.05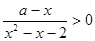
 粤公网安备 44130202000953号
粤公网安备 44130202000953号