如图1是一张折叠椅子，图2是其侧面示意图，已知椅子折叠时长1.2米，椅子展开后最大张角∠CBD＝37°，且BD＝BC，AB：BG：GC＝1：2：3，座面EF与地面平行，当展开角最大时，请解答下列问题：
（1）求∠CGF的度数；
（2）求座面EF与地面之间的距离。（可用计算器计算，结果保留两个有效数字，参考数据：sin71.5°≈0.948，cos71.5°≈0.317，tan71.5°≈2.989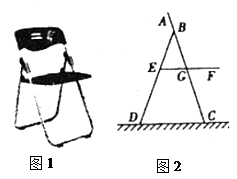
相关试题
已知一次函数y＝kx＋b的图象经过点（0，4）与点（1，2）．
（1）求一次函数的解析式；
（2）若一次函数y＝kx＋b的图象还经过点（－1，m）与点（3，n），试比较m，n的大小．
，其中x＝－
，y＝－2．
；
．
－
＋
)÷
．相关知识点
推荐套卷
粤公网安备 44130202000953号