如图，公园有一块边长为2的等边△ABC的边角地，现修成草坪， 图中DE把草坪分成面积相等的两部分，D在AB上，E在AC上．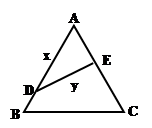
（1）设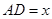
（x≥0），
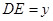，求用
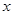表示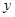
的函数关系式,并求函数的定义域；
（2）．如果
是灌溉水管，为节约成本，希望它最短，的位置应在哪里？如果是参观线路，则希望它最长，的位置又应在哪里？请予证明．
，
，求
的范围；（2）不等式
对任意
恒成立，求实数
的取值范围。
的函数
的最小值为
，试确定满足
的
的值，并对此时的
的最大值。
（Ⅰ）求函数
的最小正周期；（Ⅱ）求函数
上的最大值和最小值.
，
．
，求
的单调的递减区间；
，求
的值．
，试求式子
的值．推荐套卷
如图，公园有一块边长为2的等边△ABC的边角地，现修成草坪， 图中DE把草坪分成面积相等的两部分，D在AB上，E在AC上．
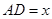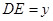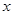（1）设（x≥0），，求用表示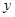的函数关系式,并求函数的定义域；
（2）．如果是灌溉水管，为节约成本，希望它最短，的位置应在哪里？如果是参观线路，则希望它最长，的位置又应在哪里？请予证明．
粤公网安备 44130202000953号