如图，已知四棱锥P-ABCD的底面为直角梯形，AD∥BC，∠BCD=900，
PA=PB，PC=PD．
（1）试判断直线CD与平面PAD是否垂直，并简述理由；
（2）求证：平面PAB⊥平面ABCD；
（3）如果CD=AD+BC，二面角P-CB-A等于600，求二面角P-CD-A的大小．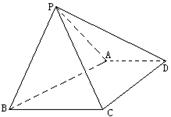
相关试题
(θ为参数,0≤θ<2π)上求一点,使它到直线C2:
(t为参数)的距离最小,并求出该点坐标和最小距离.
(θ为参数)的弦,使M为弦的中点,求此弦所在直线的方程.
(t为参数)和圆C的极坐标方程:ρ=2
sin(θ+
),判断直线和圆C的位置关系.
(0≤θ<π)和
(t∈R),求它们的交点坐标.
(t为参数),直线l2的方程为y=3x+4,求l1与l2间的距离.相关知识点
推荐套卷
如图，已知四棱锥P-ABCD的底面为直角梯形，AD∥BC，∠BCD=900，
PA=PB，PC=PD．
（1）试判断直线CD与平面PAD是否垂直，并简述理由；
（2）求证：平面PAB⊥平面ABCD；
（3）如果CD=AD+BC，二面角P-CB-A等于600，求二面角P-CD-A的大小．
粤公网安备 44130202000953号