随机观测生产某种零件的某工厂 名工人的日加工零件数(单位:件),获得数据如下:
名工人的日加工零件数(单位:件),获得数据如下: 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 ,根据上述数据得到样本的频率分布表如下:
,根据上述数据得到样本的频率分布表如下:
| 分组 |
频数 |
频率 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|
 |
 |
(1)确定样本频率分布表中的值;
(2)根据上述频率分布表,画出样本频率分布直方图;
(3)根据样本频率分布直方图,求在该厂任取 人,至少有
人,至少有 人的日加工零件数落在区间
人的日加工零件数落在区间 的概率.
的概率.
相关知识点
推荐套卷
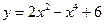 的极值。
的极值。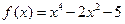 的单调区间与极值。
的单调区间与极值。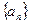 中,
中, 且点
且点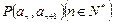 在直线
在直线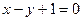 上.(1)求数列
上.(1)求数列 的通项公式;(2)若函数
的通项公式;(2)若函数 求函数
求函数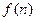 的最小值;(3)设
的最小值;(3)设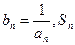 表示数列
表示数列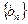 的前项和.试问:是否存在关于
的前项和.试问:是否存在关于 的整式
的整式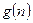 ,使得
,使得 对于一切不小于2的自然数
对于一切不小于2的自然数 上的三点,其中点A的坐标为
上的三点,其中点A的坐标为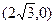 ,BC过椭圆m的中心,且
,BC过椭圆m的中心,且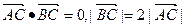 .(1)求椭圆
.(1)求椭圆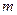 的方程;(2)过点
的方程;(2)过点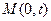 的直线l(斜率存在时)与椭圆m交于两点P,Q,设D为椭圆m与y轴负半轴的交点,且
的直线l(斜率存在时)与椭圆m交于两点P,Q,设D为椭圆m与y轴负半轴的交点,且 .求实数t的取值范围.
.求实数t的取值范围.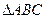 中,已知内角
中,已知内角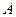 、
、 、
、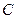 所对的边分别为
所对的边分别为 、
、 、
、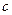 ,向量
,向量 ,且向量
,且向量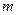 ,
, 共线.
共线.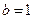 ,求
,求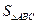 的最大值.
的最大值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号