为了了解某校学生的身高情况，随机抽取该校男生、女生进行抽样调查．已知抽取的样本中，男生、女生的人数相同，利用所得数据绘制如下统计图表：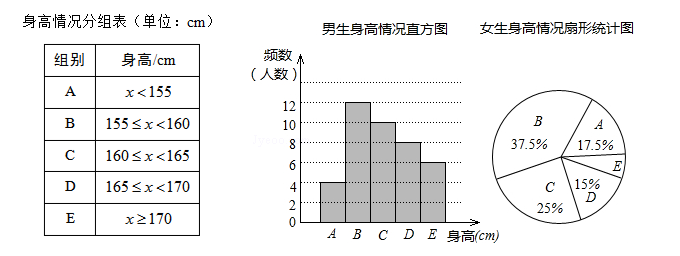
根据图表提供的信息，回答下列问题：
（1）样本中，男生的身高中位数在 组；
（2）样本中，女生身高在E组的人数有 人；
（3）已知该校共有男生800人，女生760人，请估计身高在
之间的学生约有多少人？
相关试题
，甲因看错a，解得
，乙将
其中一个方程的b写成了它的相反数，解得
，求a、b的值．
，xyz≠0，求
的值．
与
有相同的解, 求a的值和这个相同的解.相关知识点
推荐套卷
为了了解某校学生的身高情况，随机抽取该校男生、女生进行抽样调查．已知抽取的样本中，男生、女生的人数相同，利用所得数据绘制如下统计图表：
根据图表提供的信息，回答下列问题：
（1）样本中，男生的身高中位数在 组；
（2）样本中，女生身高在E组的人数有 人；
（3）已知该校共有男生800人，女生760人，请估计身高在之间的学生约有多少人？
粤公网安备 44130202000953号