某企业生产A，B两种产品，生产每吨产品所需的劳动力和煤、电耗如下表：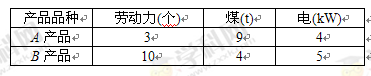
已知生产每吨A产品的利润是5万元，生产每吨B产品的利润是10万元，现因条件限制，该企业仅有劳动力300个，煤360 t，并且供电局只能供电200 kW，试问该企业生产A，B两种产品各多少吨，才能获得最大利润？
相关试题
中，
分别是角
的对边，且
.
的大小；
，求
：实数
满足
，其中
，命题
：实数
或
，且 
的取值范围.
中，角A、B、C的对边分别为
，已知向量
且满足
，（1）求角A的大小；
试判断
，点N在AC上，且AN＝2NC，AM与BN相交于点P，AP=λAM，求(1)λ的值 (2)
、
、
为
的三内角，且其对边分别为
、
、
，若
．
，求推荐套卷
某企业生产A，B两种产品，生产每吨产品所需的劳动力和煤、电耗如下表：
已知生产每吨A产品的利润是5万元，生产每吨B产品的利润是10万元，现因条件限制，该企业仅有劳动力300个，煤360 t，并且供电局只能供电200 kW，试问该企业生产A，B两种产品各多少吨，才能获得最大利润？
粤公网安备 44130202000953号