某水产养殖场拟造一个无盖的长方体水产养殖网箱，为了避免混养，箱中要安装一些筛网，其平面图如下，如果网箱四周网衣（图中实线部分）建造单价为每米56元，筛网（图中虚线部分）的建造单价为每米48元，网箱底面面积为160平方米，建造单价为每平方米50元，网衣及筛网的厚度忽略不计.
（1）把建造网箱的总造价y（元）表示为网箱的长x（米）的函数，并求出最低造价；
（2）若要求网箱的长不超过15米，宽不超过12米，则当网箱的长和宽各为多少米时，可使总造价最低？（结果精确到0.01米）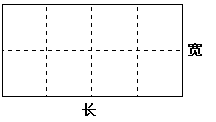
相关试题
（本题14分）在五棱锥P-ABCDE中，PA=AB=AE=2，PB=PE=
，BC=DE=1，∠EAB=∠ABC=∠DEA=90°．
（1）求证：PA⊥平面ABCDE；
（2）求二面角A-PD-E平面角的余弦值.
中，
与
都是等比数列；
的和为
，令
，求数列
的最大项.
的值；
的值.
时，试判断函数
的单调性；
时，对于任意的
，恒有
，求
的最大值．
的焦点F到直线
的距离为
．
轴的直线分别交
和
于点
.
．推荐套卷
粤公网安备 44130202000953号