已知动点P,Q都在曲线C: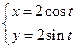 
(t为参数)上,对应参数分别为t=
与t=2 (0<<2π),M为PQ的中点.
(1)求M的轨迹的参数方程;
(2)将M到坐标原点的距离d表示为的函数,并判断M的轨迹是否过坐标原点.
的定义域为
，且同时满足下列条件：（1）
求
的取值范围。
反比例函数
，二次函数
的单调性。
是定义在区间
上的偶函数，命题
：
上单调递减；命题
：
，若“
或
的取值范围。
的图象全在
轴的上方成立的充要条件。
至少有一个负实根的充要条件。相关知识点
推荐套卷
已知动点P,Q都在曲线C: 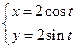(t为参数)上,对应参数分别为t=与t=2 (0<<2π),M为PQ的中点.
(1)求M的轨迹的参数方程;
(2)将M到坐标原点的距离d表示为的函数,并判断M的轨迹是否过坐标原点.
粤公网安备 44130202000953号