已知函数f(x)=ax2+4(a为非零实数),设函数F(x)=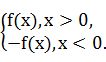
(1)若f(-2)=0,求F(x)的表达式.
(2)在(1)的条件下,解不等式1≤|F(x)|≤2.
(3)设mn<0,m+n>0,试判断F(m)+F(n)能否大于0?
推荐套卷
已知函数f(x)=ax2+4(a为非零实数),设函数F(x)=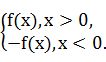
(1)若f(-2)=0,求F(x)的表达式.
(2)在(1)的条件下,解不等式1≤|F(x)|≤2.
(3)设mn<0,m+n>0,试判断F(m)+F(n)能否大于0?