如图①,在△ABC中,AB=AC,∠BAC=90°,D、E分别是AB、AC边的中点,将△ABC绕点A顺时针旋转α角(0°<α<180°),得到△AB′C′(如图②).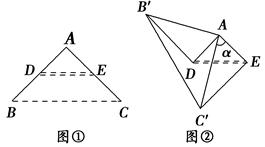
(1)探究DB′与EC′的数量关系,并给予证明;
(2)当DB′∥AE时,试求旋转角α的度数.
相关知识点
推荐套卷
如图①,在△ABC中,AB=AC,∠BAC=90°,D、E分别是AB、AC边的中点,将△ABC绕点A顺时针旋转α角(0°<α<180°),得到△AB′C′(如图②).
(1)探究DB′与EC′的数量关系,并给予证明;
(2)当DB′∥AE时,试求旋转角α的度数.