如图,已知椭圆Γ: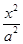 +
+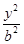 =1(a>b>0)的左、右焦点分别是F1(-c,0)、F2(c,0),Q是椭圆外的一个动点,满足|
=1(a>b>0)的左、右焦点分别是F1(-c,0)、F2(c,0),Q是椭圆外的一个动点,满足|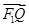 |=2a.点P是线段F1Q与该椭圆的交点,点M在线段F2Q上,且满足
|=2a.点P是线段F1Q与该椭圆的交点,点M在线段F2Q上,且满足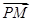 ·
·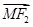 =0,|
=0,|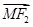 |≠0.
|≠0.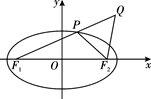
(Ⅰ)求点M的轨迹C的方程;
(Ⅱ)设不过原点O的直线l与轨迹C交于A,B两点,若直线OA,AB,OB的斜率依次成等比数列,求△OAB面积的取值范围;
(Ⅲ)由(Ⅱ)求解的结果,试对椭圆Γ写出类似的命题.(只需写出类似的命题,不必说明理由)
推荐套卷
如图,已知椭圆Γ: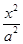 +
+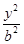 =1(a>b>0)的左、右焦点分别是F1(-c,0)、F2(c,0),Q是椭圆外的一个动点,满足|
=1(a>b>0)的左、右焦点分别是F1(-c,0)、F2(c,0),Q是椭圆外的一个动点,满足|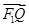 |=2a.点P是线段F1Q与该椭圆的交点,点M在线段F2Q上,且满足
|=2a.点P是线段F1Q与该椭圆的交点,点M在线段F2Q上,且满足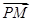 ·
·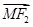 =0,|
=0,|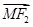 |≠0.
|≠0.
(Ⅰ)求点M的轨迹C的方程;
(Ⅱ)设不过原点O的直线l与轨迹C交于A,B两点,若直线OA,AB,OB的斜率依次成等比数列,求△OAB面积的取值范围;
(Ⅲ)由(Ⅱ)求解的结果,试对椭圆Γ写出类似的命题.(只需写出类似的命题,不必说明理由)