在计算“1×2+2×3+...+n（n+1）”时，某同学学到了如下一种方法：
先改写第k项：k（k+1）=
由此得1×2=
.
.
.............
.
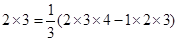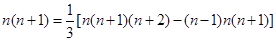相加，得1×2+2×3+...+n（n+1）
.
类比上述方法，请你计算“1×2×3×4+2×3×4×+....+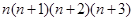
”，其结果是_________________.（结果写出关于
的一次因式的积的形式）
的值是
,
，若函数
在区间
上存在增区间，则
的取值范围为__________
的圆心在直线
上,其中
，则
的最小值是__________
满足约束条件
,则目标函数
的最大值为______
上的频数是____
相关知识点
推荐套卷
在计算“1×2+2×3+...+n（n+1）”时，某同学学到了如下一种方法：
先改写第k项：k（k+1）=
由此得1×2=..
..............
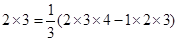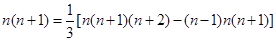相加，得1×2+2×3+...+n（n+1）.
类比上述方法，请你计算“1×2×3×4+2×3×4×+....+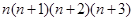”，其结果是_________________.（结果写出关于的一次因式的积的形式）
粤公网安备 44130202000953号