我们把一系列向量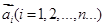 排成一列,称为向量列,记作
排成一列,称为向量列,记作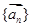 ,又设
,又设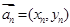 ,假设向量列
,假设向量列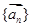 满足:
满足: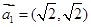 ,
,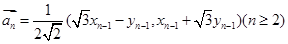 。
。
(1)证明数列 是等比数列;
是等比数列;
(2)设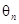 表示向量
表示向量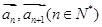 间的夹角,若
间的夹角,若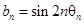 ,记
,记 的前
的前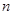 项和为
项和为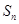 ,求
,求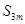 ;
;
(3)设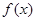 是
是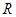 上不恒为零的函数,且对任意的
上不恒为零的函数,且对任意的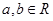 ,都有
,都有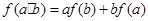 ,若
,若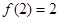 ,
, ,求数列
,求数列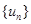 的前
的前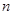 项和
项和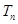 .
.
相关知识点
推荐套卷
我们把一系列向量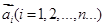 排成一列,称为向量列,记作
排成一列,称为向量列,记作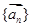 ,又设
,又设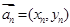 ,假设向量列
,假设向量列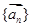 满足:
满足: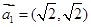 ,
,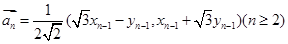 。
。
(1)证明数列 是等比数列;
是等比数列;
(2)设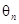 表示向量
表示向量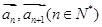 间的夹角,若
间的夹角,若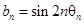 ,记
,记 的前
的前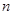 项和为
项和为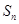 ,求
,求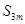 ;
;
(3)设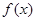 是
是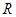 上不恒为零的函数,且对任意的
上不恒为零的函数,且对任意的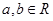 ,都有
,都有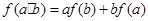 ,若
,若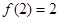 ,
, ,求数列
,求数列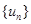 的前
的前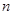 项和
项和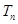 .
.