已知椭圆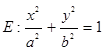
（a＞b＞0）的离心率为
，且过点（
）．
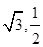（1）求椭圆E的方程；
（2）设直线l:y=kx+t与圆
（1＜R＜2）相切于点A，且l与椭圆E只有一个公共点B.
①求证：
；
②当R为何值时，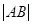
取得最大值？并求出最大值．
相关试题
中，底面
是矩形，
分别是
的中点，
平面
，
.
平面
；
．
.
，试确定函数
的单调区间；
，且对于任意
，
恒成立，试确定实数
的取值范围；
，求证：
.
求函数
的单调区间；
上的最小值为
，求
的值；
在
上恒成立，求
中，角
分别对应边
，已知
.
，求
的值；
的值.
，
.
的极大值和极小值; 
的切线的方程；
所围成的封闭图形的面积.推荐套卷
已知椭圆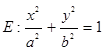（a＞b＞0）的离心率为，且过点（）．
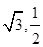（1）求椭圆E的方程；
（2）设直线l:y=kx+t与圆（1＜R＜2）相切于点A，且l与椭圆E只有一个公共点B.
①求证：；
②当R为何值时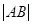，取得最大值？并求出最大值．
粤公网安备 44130202000953号