某批次的某种灯泡共 个,对其寿命进行追踪调查,将结果列成频率分布表如下.根据寿命将灯泡分成优等品、正品和次品三个等级,其中寿命大于或等于
个,对其寿命进行追踪调查,将结果列成频率分布表如下.根据寿命将灯泡分成优等品、正品和次品三个等级,其中寿命大于或等于 天的灯泡是优等品,寿命小于
天的灯泡是优等品,寿命小于 天的灯泡是次品,其余的灯泡是正品.
天的灯泡是次品,其余的灯泡是正品.
| 寿命(天) |
频数 |
频率 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| 合计 |
 |
 |
(1)根据频率分布表中的数据,写出 、
、 、
、 的值;
的值;
(2)某人从这 个灯泡中随机地购买了
个灯泡中随机地购买了 个,求此灯泡恰好不是次品的概率;
个,求此灯泡恰好不是次品的概率;
(3)某人从这批灯泡中随机地购买了 个,如果这
个,如果这 个灯泡的等级情况恰好与按三个等级分层抽样所得的结果相同,求
个灯泡的等级情况恰好与按三个等级分层抽样所得的结果相同,求 的最小值.
的最小值.
推荐套卷
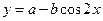
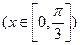 的最大值为1,最小值为
的最大值为1,最小值为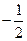 ,
, 求实数
求实数 与
与 的值。
的值。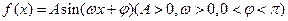
 的解析式;(2)写出
的解析式;(2)写出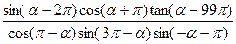 ; (Ⅱ)
; (Ⅱ)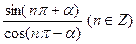
 .
. ;
; 的最小值.
的最小值. 中,直线
中,直线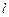 的参数方程为
的参数方程为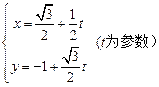 ,曲线C的参数方程为
,曲线C的参数方程为 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号