已知椭圆
的中心在原点、焦点在
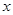轴上，抛物线
的顶点在原点、焦点在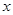轴上.小明从曲线、上各取若干个点（每条曲线上至少取两个点），并记录其坐标（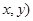
.由于记录失误，使得其中恰有一个点既不在椭圆上，也不在抛物线上，小明的记录如下：
|
 |
 |
 |
 |
 |
 |
 |
|
|
 |
 |
 |
 |
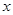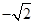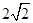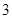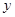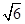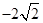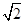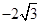据此，可推断椭圆的方程为
的夹角为120º，则
、
是非零向量，若
，则
为
与
的和向量，且
，
则
ABCD中，已知
，
，则
_______，
_______。
|=2,|
|=8,则|
|的最小值是。推荐套卷
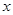已知椭圆的中心在原点、焦点在轴上，抛物线的顶点在原点、焦点在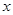轴上.小明从曲线、上各取若干个点（每条曲线上至少取两个点），并记录其坐标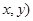（.由于记录失误，使得其中恰有一个点既不在椭圆上，也不在抛物线上，小明的记录如下：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
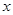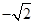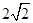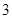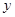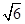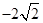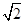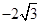据此，可推断椭圆的方程为
粤公网安备 44130202000953号