在平面直角坐标系xOy中,抛物线的解析式是y=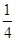 x2+1,点C的坐标为(-4,0),平行四边形OABC的顶点A,B在抛物线上,AB与y轴交于点M,已知点Q(x,y)在抛物线上,点P(t,0)在x轴上.
x2+1,点C的坐标为(-4,0),平行四边形OABC的顶点A,B在抛物线上,AB与y轴交于点M,已知点Q(x,y)在抛物线上,点P(t,0)在x轴上.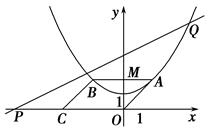
(1)写出点M的坐标;
(2)当四边形CMQP是以MQ,PC为腰的梯形时;
①求t关于x的函数解析式和自变量x的取值范围;
②当梯形CMQP的两底的长度之比为1∶2时,求t的值.
相关知识点
推荐套卷
在平面直角坐标系xOy中,抛物线的解析式是y=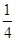 x2+1,点C的坐标为(-4,0),平行四边形OABC的顶点A,B在抛物线上,AB与y轴交于点M,已知点Q(x,y)在抛物线上,点P(t,0)在x轴上.
x2+1,点C的坐标为(-4,0),平行四边形OABC的顶点A,B在抛物线上,AB与y轴交于点M,已知点Q(x,y)在抛物线上,点P(t,0)在x轴上.
(1)写出点M的坐标;
(2)当四边形CMQP是以MQ,PC为腰的梯形时;
①求t关于x的函数解析式和自变量x的取值范围;
②当梯形CMQP的两底的长度之比为1∶2时,求t的值.