已知椭圆C：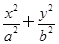
＝1(a>b>0)，点A、B分别是椭圆C的左顶点和上顶点，直线AB与圆G：x2＋y2＝
(c是椭圆的半焦距)相离，P是直线AB上一动点，过点P作圆G的两切线，切点分别为M、N.
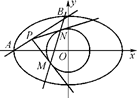
(1)若椭圆C经过两点
、
，求椭圆C的方程；
(2)当c为定值时，求证：直线MN经过一定点E，并求
·
的值(O是坐标原点)；
(3)若存在点P使得△PMN为正三角形，试求椭圆离心率的取值范围．.
推荐套卷
已知椭圆C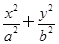：＝1(a>b>0)，点A、B分别是椭圆C的左顶点和上顶点，直线AB与圆G：x2＋y2＝(c是椭圆的半焦距)相离，P是直线AB上一动点，过点P作圆G的两切线，切点分别为M、N.
(1)若椭圆C经过两点、，求椭圆C的方程；
(2)当c为定值时，求证：直线MN经过一定点E，并求·的值(O是坐标原点)；
(3)若存在点P使得△PMN为正三角形，试求椭圆离心率的取值范围．.
粤公网安备 44130202000953号