如图,在四面体PABC中,PC⊥AB,PA⊥BC,点D,E,F,G分别是棱AP,AC,BC,PB的中点.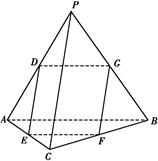
(1)求证:DE∥平面BCP.
(2)求证:四边形DEFG为矩形.
(3)是否存在点Q,到四面体PABC六条棱的中点的距离相等?说明理由.
为空间四边形
的边
上的点，且
，求证：
的底面是边长为1的正方形，
平面
是平行四边形
所在平面外一点，
、
分别是
、
的中点； 求证：
平面
平面
，
直线
，则
平面
经过平面
内一定点
，但推荐套卷
如图,在四面体PABC中,PC⊥AB,PA⊥BC,点D,E,F,G分别是棱AP,AC,BC,PB的中点.
(1)求证:DE∥平面BCP.
(2)求证:四边形DEFG为矩形.
(3)是否存在点Q,到四面体PABC六条棱的中点的距离相等?说明理由.
粤公网安备 44130202000953号