已知椭圆C:
+
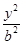=1(a>b>0),左、右两个焦点分别为F1,F2,上顶点A(0,b),△AF1F2为正三角形且周长为6.
(1)求椭圆C的标准方程及离心率;
(2)O为坐标原点,P是直线F1A上的一个动点,求|PF2|+|PO|的最小值,并求出此时点P的坐标.
相关试题
的各项均为正数，
为其前n项和，对于任意的
，满足关系式
的通项公式；
的通项公式是
，求
．
中，
，
平面
，且
，点
是
的中点.
；
的大小.
，已知
，
的值；
的值．
，使式中的
、
满足约束条件
，其相应于焦点
的准线方
；
的方程；
倾斜角为
的直线交椭圆
两点，求弦
的长度。
，求
推荐套卷
已知椭圆C:+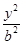=1(a>b>0),左、右两个焦点分别为F1,F2,上顶点A(0,b),△AF1F2为正三角形且周长为6.
(1)求椭圆C的标准方程及离心率;
(2)O为坐标原点,P是直线F1A上的一个动点,求|PF2|+|PO|的最小值,并求出此时点P的坐标.
粤公网安备 44130202000953号