椭圆E: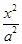
+
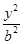=1(a>b>0)的左、右焦点分别为F1,F2,焦距为2,过F1作垂直于椭圆长轴的弦PQ,|PQ|为3.
(1)求椭圆E的方程;
(2)若过F1的直线l交椭圆于A,B两点,判断是否存在直线l使得∠AF2B为钝角,若存在,求出l的斜率k的取值范围.
相关试题
的顶点在坐标原点
，对称轴为
轴，焦点为
,抛物线上一点
的横坐标为
，且
．
做直线
交抛物线
两点，求证：
．
中，
，
，
，
⊥平面
，
，
分别是
，
的中点．
⊥平面
；
平面
，求证
；
的体积
．
，且
的通项公式；
，求适合方程
的正整数
的值．
中，已知
．
，求
的最大值．
（
为自然对数的底数）．
，
恒成立，求实数
的取值范围；
，
（
，
，
）．问：
，对任意给定的正整数
（
），都有
成立？若存在，推荐套卷
椭圆E: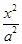+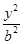=1(a>b>0)的左、右焦点分别为F1,F2,焦距为2,过F1作垂直于椭圆长轴的弦PQ,|PQ|为3.
(1)求椭圆E的方程;
(2)若过F1的直线l交椭圆于A,B两点,判断是否存在直线l使得∠AF2B为钝角,若存在,求出l的斜率k的取值范围.
粤公网安备 44130202000953号