已知△ABC的三边长|AB|= ,|BC|=4,|AC|=1,动点M满足
,|BC|=4,|AC|=1,动点M满足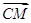 =λ
=λ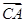 +μ
+μ ,且λμ=
,且λμ= .
.
(1)求|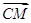 |最小值,并指出此时
|最小值,并指出此时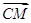 与
与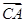 ,
, 的夹角;
的夹角;
(2)是否存在两定点F1,F2使||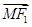 |-|
|-| ||恒为常数k?若存在,指出常数k的值,若不存在,说明理由.
||恒为常数k?若存在,指出常数k的值,若不存在,说明理由.
推荐套卷
已知△ABC的三边长|AB|= ,|BC|=4,|AC|=1,动点M满足
,|BC|=4,|AC|=1,动点M满足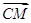 =λ
=λ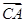 +μ
+μ ,且λμ=
,且λμ= .
.
(1)求|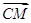 |最小值,并指出此时
|最小值,并指出此时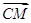 与
与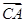 ,
, 的夹角;
的夹角;
(2)是否存在两定点F1,F2使||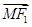 |-|
|-| ||恒为常数k?若存在,指出常数k的值,若不存在,说明理由.
||恒为常数k?若存在,指出常数k的值,若不存在,说明理由.