已知定点A(－2,0)和B(2,0)，曲线E上任一点P满足|PA|－|PB|＝2.
（1）求曲线E的方程；
（2）延长PB与曲线E交于另一点Q，求|PQ|的最小值；
（3）若直线l的方程为x＝a(a≤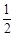
)，延长PB与曲线E交于另一点Q，如果存在某一位置，使得从PQ的中点R向l作垂线，垂足为C，满足PC⊥QC，求a的取值范围。
相关试题
过点（0，4），离心率为
.
的直线被C所截得线段的中点坐标.
前
项和为
，且
（
）求数列
前
时，可以选与塔底
同一水平面内的两个测点
.现测得
，
，并在点
测得塔顶
的仰角为
， 求塔高
，
）
在
时取得最大值4． 
的最小正周期；
(
α +
)=
,求sinα．
，
的单调区间。
）处的切线的倾斜角为
，对任意的
,函数
在区间
上总不是单调函数，求m取值范围
相关知识点
推荐套卷
已知定点A(－2,0)和B(2,0)，曲线E上任一点P满足|PA|－|PB|＝2.
（1）求曲线E的方程；
（2）延长PB与曲线E交于另一点Q，求|PQ|的最小值；
（3）若直线l的方程为x＝a(a≤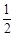)，延长PB与曲线E交于另一点Q，如果存在某一位置，使得从PQ的中点R向l作垂线，垂足为C，满足PC⊥QC，求a的取值范围。
粤公网安备 44130202000953号