某人在汽车站M的北偏西20°的方向上的A处(如图所示)，观察到C处有一辆汽车沿公路向M站行驶，公路的走向是M站的北偏东40°.开始时，汽车到A处的距离为31km，汽车前进20km后，到A处的距离缩短了10km.问汽车还需行驶多远，才能到达汽车站M?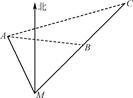
相关试题
=
，
=
、
及向量
的坐标；
．
的顶点
、
、
，求顶点
的标．
=（1，
），
=（
，1），
=
=2
满足
为等比数列；
以及前n项和
；
都有
求
的取值范围。
中，已知
。
和前n项和
；
的值；
的前n项和
.推荐套卷
某人在汽车站M的北偏西20°的方向上的A处(如图所示)，观察到C处有一辆汽车沿公路向M站行驶，公路的走向是M站的北偏东40°.开始时，汽车到A处的距离为31km，汽车前进20km后，到A处的距离缩短了10km.问汽车还需行驶多远，才能到达汽车站M?
粤公网安备 44130202000953号