已知ω>0,a=(2sinωx+cosωx,2sinωx-cosωx),b=(sinωx,cosωx).f(x)=a·b.f(x)图象上相邻的两个对称轴的距离是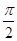 .
.
(1)求ω的值;
(2)求函数f(x)在区间 上的最大值和最小值.
上的最大值和最小值.
相关知识点
推荐套卷
已知ω>0,a=(2sinωx+cosωx,2sinωx-cosωx),b=(sinωx,cosωx).f(x)=a·b.f(x)图象上相邻的两个对称轴的距离是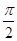 .
.
(1)求ω的值;
(2)求函数f(x)在区间 上的最大值和最小值.
上的最大值和最小值.