对实数a和b,定义运算“⊗”:a⊗b=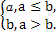
设函数f(x)=(x2-1)⊗(x-x2),x∈R.若函数y=f(x)-c恰有两个不同的零点,则实数c的取值范围是( )
A．(-∞,-1)∪(- ,0) |
B．{-1,-} |
| C．(-1,-) |
D．(-∞,-1)∪[-,0) |
的公差
在区间
上是减少的，那么实数
的取值范围是（）
求
（
为虚数单位）的实部为
的定义域为（）
}相关知识点
推荐套卷
对实数a和b,定义运算“⊗”:a⊗b=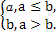设函数f(x)=(x2-1)⊗(x-x2),x∈R.若函数y=f(x)-c恰有两个不同的零点,则实数c的取值范围是( )
| A．(-∞,-1)∪(-,0) |
B．{-1,-} |
| C．(-1,-) |
D．(-∞,-1)∪[-,0) |
粤公网安备 44130202000953号