如图,AA1,BB1为圆柱OO1的母线,BC是底面圆O的直径,D,E分别是AA1,CB1的中点,DE⊥面CBB1.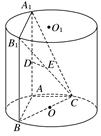
(1)证明:DE∥面ABC;
(2)求四棱锥CABB1A1与圆柱OO1的体积比.
相关知识点
推荐套卷
如图,AA1,BB1为圆柱OO1的母线,BC是底面圆O的直径,D,E分别是AA1,CB1的中点,DE⊥面CBB1.
(1)证明:DE∥面ABC;
(2)求四棱锥CABB1A1与圆柱OO1的体积比.