已知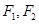 为椭圆
为椭圆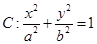
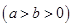 的左右焦点,
的左右焦点,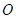 是坐标原点,过
是坐标原点,过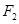 作垂直于
作垂直于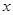 轴的直线
轴的直线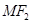 交椭圆于
交椭圆于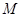 ,设
,设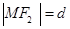 .
.
(1)证明: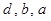 成等比数列;
成等比数列;
(2)若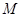 的坐标为
的坐标为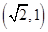 ,求椭圆
,求椭圆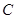 的方程;
的方程;
(3)在(2)的椭圆中,过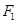 的直线
的直线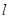 与椭圆
与椭圆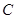 交于
交于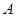 、
、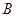 两点,若
两点,若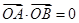 ,求直线
,求直线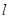 的方程.
的方程.
推荐套卷
已知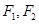 为椭圆
为椭圆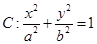
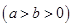 的左右焦点,
的左右焦点,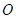 是坐标原点,过
是坐标原点,过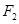 作垂直于
作垂直于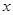 轴的直线
轴的直线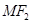 交椭圆于
交椭圆于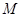 ,设
,设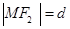 .
.
(1)证明: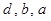 成等比数列;
成等比数列;
(2)若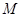 的坐标为
的坐标为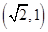 ,求椭圆
,求椭圆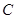 的方程;
的方程;
(3)在(2)的椭圆中,过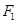 的直线
的直线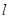 与椭圆
与椭圆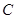 交于
交于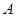 、
、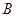 两点,若
两点,若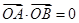 ,求直线
,求直线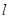 的方程.
的方程.