某校高一年级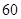
名学生参加数学竞赛，成绩全部在
分至
分之间，现将成绩分成以下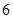
段：
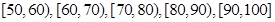，据此绘制了如图所示的频率分布直方图. 
（1）求成绩在区间
的频率；
（2）从成绩大于等于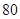
分的学生中随机选
名学生，其中成绩在
内的学生人数为
，求的分布列与均值.
，
，若
且
，求
的值
.
＋f(x)＝0.
, x∈[3, 5]
｝，B={x|
}，求
，
。
，求a；推荐套卷
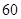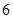某校高一年级名学生参加数学竞赛，成绩全部在分至分之间，现将成绩分成以下段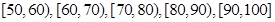：，据此绘制了如图所示的频率分布直方图.
（1）求成绩在区间的频率；
（2）从成绩大于等于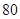分的学生中随机选名学生，其中成绩在内的学生人数为，求的分布列与均值.
粤公网安备 44130202000953号