如图,在三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.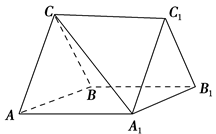
(1)证明:AB⊥A1C;
(2)若AB=CB=2,A1C=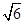 ,求三棱柱ABC-A1B1C1的体积;
,求三棱柱ABC-A1B1C1的体积;
(3)若平面ABC⊥平面AA1B1B,AB=CB=2,求直线A1C与平面BB1C1C所成角的正弦值.
相关知识点
推荐套卷
如图,在三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.
(1)证明:AB⊥A1C;
(2)若AB=CB=2,A1C=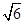 ,求三棱柱ABC-A1B1C1的体积;
,求三棱柱ABC-A1B1C1的体积;
(3)若平面ABC⊥平面AA1B1B,AB=CB=2,求直线A1C与平面BB1C1C所成角的正弦值.