有形状、大小和质地都相同的四张卡片,正面分别写有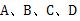 和一个等式,将这四张卡片背面向上洗匀,从中随机抽取一张(不放回),接着再随机抽取一张.
和一个等式,将这四张卡片背面向上洗匀,从中随机抽取一张(不放回),接着再随机抽取一张.
(1)用画树状图或列表的方法表示抽取两张卡片可能出现的所有情况(结果用A、B、C、D表示);
(2)小明和小强按下面规则做游戏:抽取的两张卡片上若等式都不成立,则小明胜,若至少有一个等式成立,则小强胜.你认为这个游戏公平吗?若公平,请说明理由;若不公平,则这个规则对谁有利,为什么?
相关知识点
推荐套卷
有形状、大小和质地都相同的四张卡片,正面分别写有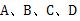 和一个等式,将这四张卡片背面向上洗匀,从中随机抽取一张(不放回),接着再随机抽取一张.
和一个等式,将这四张卡片背面向上洗匀,从中随机抽取一张(不放回),接着再随机抽取一张.
(1)用画树状图或列表的方法表示抽取两张卡片可能出现的所有情况(结果用A、B、C、D表示);
(2)小明和小强按下面规则做游戏:抽取的两张卡片上若等式都不成立,则小明胜,若至少有一个等式成立,则小强胜.你认为这个游戏公平吗?若公平,请说明理由;若不公平,则这个规则对谁有利,为什么?