如图所示，在棱长为2的正方体ABCD－A1B1C1D1中，O是底面ABCD的中心，E、F分别是CC1、AD的中点．那么异面直线OE和FD1所成的角的余弦值等于 ( )．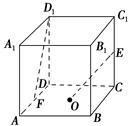
A． |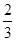
B． |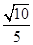
C． |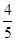
D． |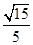
相关试题
的小正方形，在其上用粗线画出了一四棱锥的三视图，则该四棱锥的体积为（）
表示面积为
的直角三角形区域，则实数
的值为（）
的离心率为
，则其渐近线的斜率为（）
，
，则
（）
”是“函数
为奇函数” 的（）推荐套卷
如图所示，在棱长为2的正方体ABCD－A1B1C1D1中，O是底面ABCD的中心，E、F分别是CC1、AD的中点．那么异面直线OE和FD1所成的角的余弦值等于 ( )．
| A． |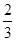
B． |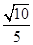
C． |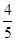
D． |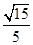
粤公网安备 44130202000953号