甲、乙两名教师进行乒乓球比赛,采用七局四胜制(先胜四局者获胜).若每一局比赛甲获胜的概率为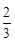
,乙获胜的概率为
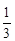,现已赛完两局,乙暂时以2∶0领先.
(1)求甲获得这次比赛胜利的概率；
(2)设比赛结束时比赛的局数为随机变量X，求随机变量X的概率分布和数学期望EX.
相关试题
最值.
＞0）
的一个极值点，求
的值；
上是增函数；
总存在
＞
成立，求实数m的取值范围。
举行环保知识大奖赛，比赛分初赛和决赛两部分，初赛采用选手选一题答一题的方式进行，每位选手最多有5次选题答题的机会，选手累计答对3题或答错3题即终止其初赛的比赛，答对3题者直接进入决赛，答错3题者则被淘汰，已知选手甲答题连续两次答错的概率为
（已知甲回答每个问题的正确率相同，并且相互之间没有影响）.
，试写出推荐套卷
甲、乙两名教师进行乒乓球比赛,采用七局四胜制(先胜四局者获胜).若每一局比赛甲获胜的概率为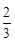,乙获胜的概率为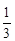,现已赛完两局,乙暂时以2∶0领先.
(1)求甲获得这次比赛胜利的概率；
(2)设比赛结束时比赛的局数为随机变量X，求随机变量X的概率分布和数学期望EX.
粤公网安备 44130202000953号