制作一种产品,需先将材料加热达到60 ℃后,再进行操作.设该材料温度为y(℃),从加热开始计算的时间为x(min).据了解,当该材料加热时,温度y与时间x成一次函数关系;停止加热进行操作时,温度y与时间x成反比例关系(如图).已知该材料在操作加热前的温度为15 ℃,加热5分钟后温度达到60 ℃.
(1)分别求出将材料加热和停止加热进行操作时,y与x的函数关系式;
(2)根据工艺要求,当材料的温度低于15 ℃时,须停止操作,那么从开始加热到停止操作,共经历了多少时间?
相关知识点
推荐套卷
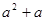 ,宽为
,宽为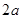 的长方形铁皮,将其四个角分别剪去一个边长为
的长方形铁皮,将其四个角分别剪去一个边长为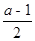 (
( >1)的正方形,剩余的部分可制成一个无盖的长方体盒子。(损失的忽略不计)则长方体盒子的底面的长AB= ,AD= .求这个盒子的容积
>1)的正方形,剩余的部分可制成一个无盖的长方体盒子。(损失的忽略不计)则长方体盒子的底面的长AB= ,AD= .求这个盒子的容积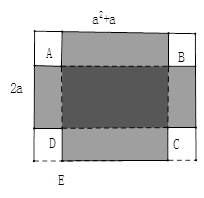
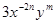 与
与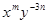 的积与
的积与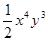 是同类项,求
是同类项,求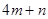 的平方根
的平方根 ,
,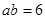 .求:
.求: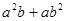 的值;
的值;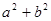 的值.
的值. ,其中
,其中 =
= 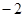

 粤公网安备 44130202000953号
粤公网安备 44130202000953号