如图所示，在△ABC中，AB=AC，AD是△ABC的角平分线，DE⊥AB，DF⊥AC，垂足分别是E，F．则下列结论：①DA平分∠EDF；②AE=AF，DE=DF；③AD上的点到B，C两点的距离相等；④图中共有3对全等三角形，正确的有 .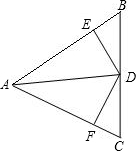
，则a= ．相关知识点
推荐套卷
如图所示，在△ABC中，AB=AC，AD是△ABC的角平分线，DE⊥AB，DF⊥AC，垂足分别是E，F．则下列结论：①DA平分∠EDF；②AE=AF，DE=DF；③AD上的点到B，C两点的距离相等；④图中共有3对全等三角形，正确的有 .
粤公网安备 44130202000953号