若连续函数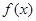 在
在 上可导,其导函数为
上可导,其导函数为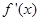 ,且函数
,且函数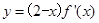 的图像如图所示,则下列结论中一定成立的是( )
的图像如图所示,则下列结论中一定成立的是( )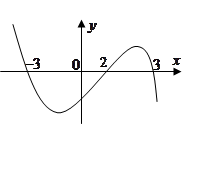
A.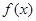 有极大值 有极大值 和极小值 和极小值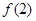 |
B.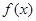 有极大值 有极大值 和极小值 和极小值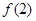 |
C.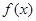 有极大值 有极大值 和极小值 和极小值 |
D.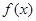 有极大值 有极大值 和极小值 和极小值 |
相关知识点
推荐套卷
若连续函数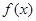 在
在 上可导,其导函数为
上可导,其导函数为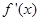 ,且函数
,且函数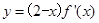 的图像如图所示,则下列结论中一定成立的是( )
的图像如图所示,则下列结论中一定成立的是( )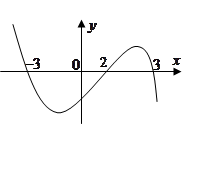
A.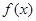 有极大值 有极大值 和极小值 和极小值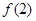 |
B.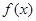 有极大值 有极大值 和极小值 和极小值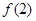 |
C.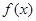 有极大值 有极大值 和极小值 和极小值 |
D.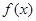 有极大值 有极大值 和极小值 和极小值 |