如图,等边△ABC的边长为4,E是边BC上的动点,EH⊥AC于H,过E作EF∥AC,交线段AB于点F,在线段AC上取点P,使PE＝EB．设EC＝x（0＜x≤2）．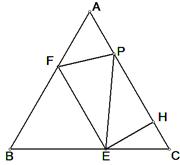
（1）请直接写出图中与线段EF相等的两条线段（不再另外添加辅助线）；
（2）Q是线段AC上的动点,当四边形EFPQ是平行四边形时,求平行四边形EFPQ的面积（用含
的代数式表示）；
（3）当（2）中 的平行四边形EFPQ面积最大值时,以E为圆心,r为半径作圆,根据⊙E与此时平行四边形EFPQ四条边交点的总个数,求相应的r的取值范围．
相关试题
－
b)－3(2a
，b=4．在等边△ABC中，点E在AB上，点D在CB的延长线上，且ED=EC.
(1)、若点E是AB的中点，如图1，求证：AE=DB.
(2)、若点E不是AB的中点时，如图2，试确定线段AE与DB的大小关系，并写出证明过程.
中，△ABC与△DEF全等，其中A、B、C的对应顶点分别为D、E、F，且AB="BC." 若A点的坐标为（
，1），B、C两点的纵坐标均为
轴上.
相关知识点
推荐套卷
粤公网安备 44130202000953号