已知：如图①,在Rt△ACB中,∠C＝90º,AC＝6cm,BC＝8cm,点P由B出发沿BC方向向点C匀速运动,速度为2cm/s；点Q由A出发沿AB方向向点B匀速运动,速度为1cm/s；连接PQ．若设运动的时间为t(s)（0＜t＜4）,解答下列问题：
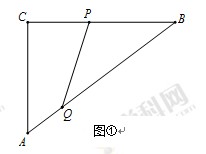
（1）当t为何值时,PQ的垂直平分线经过点B？
（2）如图②,连接CQ．设△PQC的面积为y（cm2）,求y与t之间的函数关系式；
（3）如图②,是否存在某一时刻t,使线段C Q恰好把四边形ACPQ的面积分成1：2的两部分？若存在,求出此时t的值；若不存在,说明理由.
根据卫生防疫部门要求，游泳池必须定期换水，清洗．某游泳池周五早上 打开排水孔开始排水，排水孔的排水速度保持不变，期间因清洗游泳池需要暂停排水，游泳池的水在 全部排完．游泳池内的水量 和开始排水后的时间 之间的函数图象如图所示，根据图象解答下列问题：
（1）暂停排水需要多少时间？排水孔排水速度是多少？
（2）当 时，求 关于 的函数表达式．
为了解七年级学生上学期参加社会实践活动的情况，随机抽查 市七年级部分学生参加社会实践活动天数，并根据抽查结果制作了如下不完整的频数分布表和条形统计图．
市七年级部分学生参加社会实践活动天数的频数分布表
天数 |
频数 |
频率 |
3 |
20 |
0.10 |
4 |
30 |
0.15 |
5 |
60 |
0.30 |
6 |
|
0.25 |
7 |
40 |
0.20 |
市七年级部分学生参加社会实践活动天数的条形统计图
根据以上信息，解答下列问题；
（1）求出频数分布表中 的值，并补全条形统计图．
（2） 市有七年级学生20000人，请你估计该市七年级学生参加社会实践活动不少于5天的人数．
小明的爸爸和妈妈分别驾车从家同时出发去上班，爸爸行驶到甲处时，看到前面路口时红灯，他立即刹车减速并在乙处停车等待，爸爸驾车从家到乙处的过程中，速度 与时间 的关系如图1中的实线所示，行驶路程 与时间 的关系如图2所示，在加速过程中， 与 满足表达式
（1）根据图中的信息，写出小明家到乙处的路程，并求 的值；
（2）求图2中 点的纵坐标 ，并说明它的实际意义；
（3）爸爸在乙处等待7秒后绿灯亮起继续前行，为了节约能源，减少刹车，妈妈驾车从家出发的行驶过程中，速度 与时间 的关系如图1中的折线 所示，加速过程中行驶路程 与时间 的关系也满足 ，当她行驶到甲处时，前方的绿灯刚好亮起，求此时妈妈驾车的行驶速度．
我们定义：有一组邻角相等的凸四边形叫做“等邻角四边形”
（1）概念理解：
请你根据上述定义举一个等邻角四边形的例子；
（2）问题探究：
如图1，在等邻角四边形 中， ， ， 的中垂线恰好交于 边上一点 ，连接 ， ，试探究 与 的数量关系，并说明理由；
（3）应用拓展：
如图2，在 与 中， ， ， ，将 绕着点 顺时针旋转角 得到 △ （如图 ，当凸四边形 为等邻角四边形时，求出它的面积．
粤公网安备 44130202000953号