如图1,若△ABC和△ADE为等腰直角三角形,AB=AC,AD=AE,M,N分别EB,CD的中点．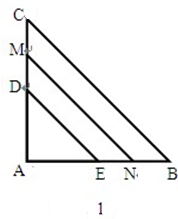
（1）易证：①CD="BE" ；②△AMN是 三角形；
（2）当把△ADE绕A点旋转到图2的位置时,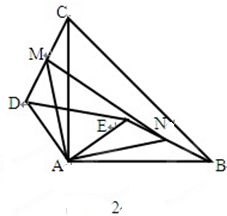
①求证：CD=BE；
②判断△AMN的形状,并证明你的结论；
（3）当△ADE绕A点旋转到图3的位置时,（2）中的结论是否成立？直接写出即可,不要求证明；并求出当AB=2AD时,△ADE与△ABC及△AMN的面积之比．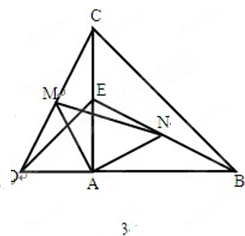
相关试题
（1）如图1，
和
都是等边三角形，且
三点共线，连接
相交于点
，求证：
．
（2）如图2，在
中，
°，分别以
和
为边在外部作等边、等边和等边
，联结和
交于点，下列结论中正确的是 （只填序号即可）
①
；②
；③
°；
（3）如图2，在（2）的条件下，求证：
．
相关知识点
推荐套卷
粤公网安备 44130202000953号